对角占优矩阵

        对角占优矩阵指矩阵的对角元素大于它所在的行或列其他元素的合计。在这一定义的基础上，对角占优概念不断扩展和延伸，特别是数理经济学家麦肯齐(Lionel McKenzie)提出了他著名的拟对角占优矩阵概念，并在这一概念的基础上进一步提出了与广义H-S定理等价的投入产出系统有经济意义解的条件。

        这里定义的是列对角占优，按照同样的方式也可以定义行对角占优。

        如果上述定义中严格不等式成立，则称为严格对角占优矩阵(strictly diagonally dominant)。严格对角占优矩阵具有某些特定的性质。例如，严格对角占优矩阵必为非奇异矩阵。正因为此，数理经济学家更为关注的是这种严格对角占优矩阵，例如在二阶堂等人的数理经济学文献中，直接把严格对角占优矩阵称为对角占优矩阵，简记为d. d.。

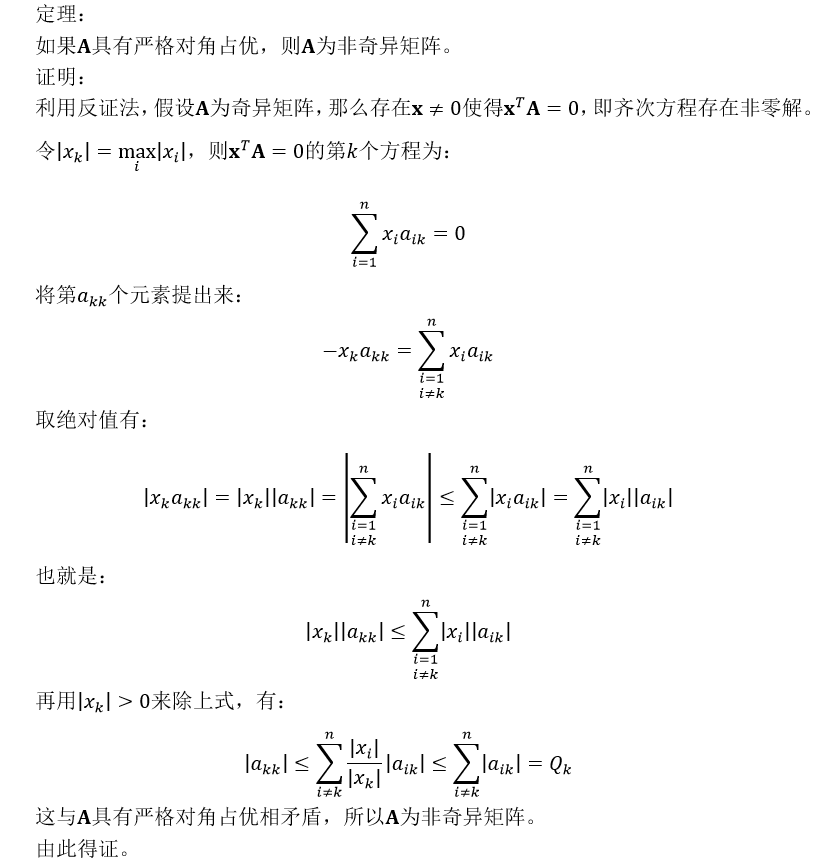
        我们看到，严格对角占优矩阵具有非奇异性，而一般的对角占优矩阵并不能保证这一性质。但是对于不可分解矩阵而言，在这些非严格不等式中如果至少有一个严格不等式成立，那么非严格的对角占优矩阵也具有非奇异的性质。

        定义：广义对角占优矩阵

        如果存在正的对角矩阵D，使得DA为严格对角占优矩阵，则称A为广义对角占优矩阵(dominant diagonal in the extended sense,简记为D. D.)。

        这一形式的广义对角占优矩阵在有些文献中也被称为拟对角占优矩阵。显然，广义对角占优矩阵也是非奇异的。因为如果方阵A为广义对角占优矩阵，那么DA将是严格对角占优矩阵，进而DA所构成的矩阵将是非奇异的。由于D矩阵是正的对角矩阵，是非奇异的，于是A也是非奇异的。

        从前面的陶斯基定理可知，将严格对角占优矩阵推广到非严格不可约对角占优矩阵，在附加至少存在一个严格不等式的条件之后，非奇异性质将得以保持。结合现在的广义对角占优矩阵，类似的结论同样成立。

        麦肯齐提出了一种更为广义的对角占优矩阵，不仅把非奇异性质推广到非严格不等式的情况，同时也推广到可分解矩阵的情形。他也把这种更为广义的对角占优矩阵称为拟对角占优矩阵(quasi-dominant diagonal,简记为q. d. d.)。无特别指明时，所称拟对角占优矩阵均指麦肯齐的这一定义。